Персональный сайт - Основные форумлы площадей треугольника, параллелограмма,трапеции

Площадь треугольника

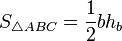$S_{\triangle ABC}= \frac {1}{2} bh_b$ , так как $\ h_b = a \sin \gamma$ , то:
$S_{\triangle ABC}=\frac {1}{2} ab \sin \gamma$
$S_{\triangle ABC}=\frac {1}{2} r(a+b+c) = pr = (p-b)r_b$
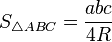
$S_{\triangle ABC}=\frac {abc}{4R}$
$S_{\triangle ABC}= \sqrt{p(p-a)(p-b)(p-c)} = {1 \over 4}\sqrt{(a+b+c)(b+c-a)(a+c-b)(a+b-c)}$ — формула Герона
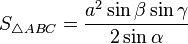
$S_{\triangle ABC}= \frac {a^2\sin\beta\sin\gamma}{2\sin\alpha}$
$S_{\triangle ABC}= {2R^2\sin\alpha\sin\beta\sin\gamma}$
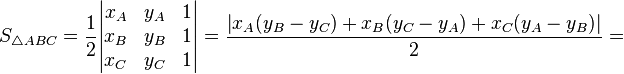
$S_{\triangle ABC}= \frac{1}{2}\begin{vmatrix} x_A & y_A & 1 \\ x_B & y_B & 1 \\ x_C & y_C & 1 \end{vmatrix}=\frac {\left|x_A(y_B-y_C)+x_B(y_C-y_A)+x_C(y_A-y_B)\right|}{2}=$
$=\frac {\left|(x_B - x_A)(y_C-y_A)-(x_C-x_A)(y_B-y_A)\right|}{2}$
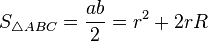$S_{\triangle ABC}=\frac{ab}{2}=r^2+2rR$ — для прямоугольного треугольника
$S=\frac {a^2\sqrt{3}}{4}$ — для равностороннего треугольника
$S_{\triangle ABC}=\frac {c^2}{2(ctg\alpha+ctg\beta)}$ — если треугольник задан по стороне и двум прилежащим к ней углам
$S_{\triangle ABC}=\frac {c^2\sin\alpha\sin\beta}{2sin(\alpha+\beta)}$ — если треугольник задан по стороне и двум прилежащим к ней углам

Где:

$\ h_b$ — высота, проведённая на сторону $\ b$ ,
$p=\frac {a+b+c}{2}$ — полупериметр,
$\ r$ — радиус вписанной окружности,
$\ r_b$ — радиус вневписанной окружности, касающейся стороны $\ b$ ,
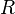$\ R$ — радиус описанной окружности

Площадь параллелограмма

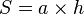$S = a \times h$ , где a - сторона, h - высота проведенная к этой стороне.

$S = a \times b \times sin \alpha$ , где a и b - стороны, а

α

— угол между сторонами a и b

$S = \frac{1}{2}AC \times BD \times sin AOB$

Площадь трапеции

В случае, если

a

и

b

— основания и

h

— высота, формула площади:

$S= \frac{(a+b)}{2}h$

В случае, если $m$ — средняя линия и $h$ — высота, формула площади:

$S= \displaystyle m h$

Формула, где $a$ , $b$ — основания, $c$ и $d$ — боковые стороны трапеции:

$S=\frac{a+b}{2}\sqrt{c^2-\left(\frac{(b-a)^2+c^2-d^2}{2(b-a)}\right)^2}$

Площадь равнобедренной трапеции с радиусом вписанной окружности равном $r$ и углом при основании $α$ :

$S=\frac{4r^2}{\sin{\alpha}}$

Обратная связь

Бесплатный хостинг uCoz