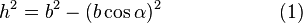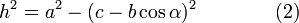Персональный сайт - Теорема косинусов для треугольника

Теорема косинусов — Для плоского треугольника со сторонами $a, b, c$ и углом $α$ , противолежащим стороне $a$ , справедливо соотношение:

$a^2 = b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos \alpha$ .

Доказательство

Рассмотрим треугольник ABC. Из вершины C на сторону AB опущена высота CD. Из треугольника ADC следует:

A D = b cosα

D B = c - b cosα

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

$h^2 = b^2 - (b \cos \alpha)^2 \qquad \qquad \qquad(1)$

$h^2 = a^2 - (c - b \cos \alpha)^2 \qquad \qquad (2)$

Приравниваем правые части уравнений (1) и (2) и:

b 2 - (b cosα) 2 = a 2 - (c - b cosα) 2

или

a 2 = b 2 + c 2 - 2 b c cosα

Обратная связь