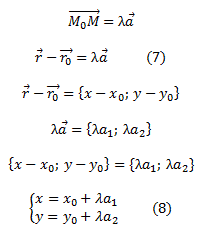Различные виды уравнения прямой

k = tg(α) – угловой коэффициент

y = kx + b            (1) – уравнение прямой с угловым коэффициентом k

1)      Если угол α острый, то tg α > 0 и k > 0

2)      Если угол α тупой, то tg α < 0 и k < 0

3)      Если прямая проходит через начало координат, то b = 0

4)      Если прямая || OX, то угол α = 0 = tg α = k = 0

5)      Если α = π/2, то tg α не существует и уравнение теряет смысл.

Вывод общего уравнения прямой.

Получим сначала уравнение прямой, проходящей через заданную точку M₀(x₀; y₀) перпендикулярно данному ненулевому вектору 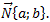Отметим на прямой точку M(x; y). Поскольку векторы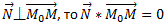

a (x – x₀) + b (y – y₀) = 0                               (2) – уравнение прямой, проходящей через заданную точку перпендикулярно данному вектору.

                Вектор 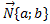 называется нормальным вектором этой прямой.

ax - ax₀ + by – by₀ = 0

ax + by + (-ax₀ – by₀) = 0

ax + by + c = 0                   (3), где a, b и c – произвольные числа, причем a² + b² <> 0

Покажем, что это действительно общее уравнение прямой:

1)      b = 0, a <> 0       =>          ax + c = 0;           x = c / a

2)      b <> 0, a <> 0    =>          y = - (a / b)x + c / b

3)      b <> 0, a = 0       =>          y = - c / b

4)      b <> 0, a <> 0, c = 0        =>          ax + by = 0;        y = -(a / b)x

Частные случаи:

Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом:

Пусть прямая проходит через точку M(x₀; y₀) и имеет угловой коэффициент k. Тогда уравнение прямой имеет вид (1). Так как прямая проходит через точку M, то ее координата должна удовлетворять уравнению (1), т.е.

                y₀ = kx₀ + b         =>          b = -kx₀ + y₀

Тогда уравнение (1) можно переписать в виде:

                y = kx – kx₀ + y₀   =>  y = k(x – x₀) + y₀                                    (4)

Уравнение прямой, проходящей через две точки:

Пусть прямая проходит через точки M₁(x₁; y₁) и M₂(x₂; y₂). Тогда используя (4) уравнение прямой, проходящей через M₁, имеет вид

                y – y₁ = k(x – x₁)                              (*), где k  - пока неизвестный коэффициент.

С другой стороны, поскольку прямая проходит через точку M₂, ее координаты также должны удовлетворять уравнению (*):

                y₂ – y₁ = k(x₂ – x₁)           (**)

Поделим (*) на (**):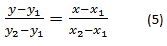

Предполагается, что в этом уравнении x₂ <> x₁ и y₂ <> y₁

Если x₂ = x₁, то тогда прямая, проходящая через точки M₁ и M₂ || Oy. Тогда уравнение имеет вид x = x₁. Если y₂ = y₁, то M₁M₂ || Ox и может быть записана в виде y = y₁

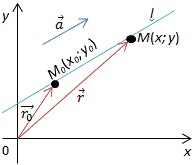
Векторное уравнение прямой:

Пусть в в прямоугольной системе координат задана некоторая точка M₀(x₀; y₀) и некоторый вектор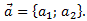

Рассмотрим прямую l, проходящую через заданную точку и параллельно вектору (вектор a  в этом случае будет называться направляющим вектором данной прямой).

Далее пусть M – любая точка прямой l. Тогда для радиус-векторов этих точек верно соотношение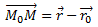

Это соотношение верно для любой точки M, лежащей на прямой l.

Кроме того, легко видеть, что 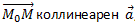, тогда верно соотношение