Бином Ньютона — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
,
где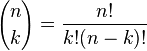 
— биномиальные коэффициенты, n — неотрицательное целое число.
Свойства:
- В разложении бинома содержится на один член больше, чем его степень.
- Разложение есть однородный многочлен, то есть все члены имеют одну и ту же степень относительно a и b
- Коэффициенты бинома
называются биномиальными и являются натуральными числами (если 
) - Общий член разложения бинома имеет вид
- Биномиальные коэффициенты, равноотстоящие от концов равны между собой
- Из свойств (1) и (5) следует, что если показатель бинома четный, то в разложении средний член имеет наибольший коэффициент, а если показатель бинома нечетный, то в разложении имеется два средних члена с одинаковым наибольшим коэффициентом
- Сумма всех биномиальных коэффициентов равна 2^n. Это следует из формулы бинома, если в ней положить, что a = b = 1
- Сумма биномиальных коэффициентов на четных местах равна сумме коэффициентов на нечетных местах
- Если a заменить на -a, то знаки перед коэффициентами будут чередоваться
