Угол между прямыми на плоскости.

  Определение.

• Если заданы две прямые y = k₁x + b₁, y = k₂x + b₂, то острый угол между этими прямыми будет определяться как.Две прямые параллельны, если k₁ = k₂.Две прямые перпендикулярны, если k₁ = -1/k₂.  
• Если две прямые заданы общими уравнениями (Ах + Ву + С = 0 и А₁х + В₁у + С₁ = 0), то угол между ними вычисляется как угол между нормальными векторами . Две прямые параллельны, когда пропорциональны коэффициенты А₁ = lА, В₁ = lВ. Если еще и С₁ = lС, то прямые совпадают.

Вывод формулы расстояния от точки до прямой

Вариант 1 

Пусть на плоскости дана прямая l : ax + by + c = 0 и точка M₁(x₁;y₁), не принадлежащая этой прямой. Найдем расстояние от точки до прямой. Под расстоянием ρ от точки M₁ до прямой l понимают длину отрезка M₀ M₁⏊l.

Для определения расстояния удобно использовать единичный вектор, коллинеарный нормальному вектору прямой.

 Пояснение: поскольку точка M₀ лежит в на прямой l, то ее координаты должны удовлетворять уравнению данной прямой, т.е. ax₀ + by₀ + c = 0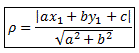Вариант 2

Если задана точка М(х₀, у₀), то расстояние до прямой Ах + Ву + С =0 определяется как .

  Доказательство. Пусть точка М₁(х₁, у₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М₁:   (1) Координаты x₁ и у₁ могут быть найдены как решение системы уравнений: Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М₀ перпендикулярно заданной прямой.  Если преобразовать первое уравнение системы к виду: A(x – x₀) + B(y – y₀) + Ax₀ + By₀ + C = 0, то, решая, получим: Подставляя эти выражения в уравнение (1), находим: . Теорема доказана.