Персональный сайт - Подобие треугольников

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны соответственным сторонам другого.

Первый признак

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.

Дано: ∆ABC и ∆A₁B₁C₁, ∠A=∠A₁, ∠B=∠B₁.

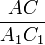$\frac{S}{S_1}$ = $\frac{AB \cdot AC}{A_1B_1 \cdot A_1C_1}$ = $\frac{AB \cdot BC}{A_1B_1 \cdot B_1C_1}$ => $\frac{AC}{A_1C_1}$ = $\frac{BC}{B_1C_1}$ .

Второй признак

Если две стороны одного треугольника пропорциональны двум сторонам другого и угол между этими сторонами в первом и втором треугольнике равен, тогда эти треугольники подобны.

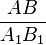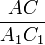Дано: ∆ABC и ∆A₁B₁C₁, ∠A=∠A₁, $\frac{AB}{A_1B_1}$ = $\frac{AC}{A_1C_1}$ .

Доказать: ∆ABC 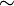$\sim$ ∆A₁B₁C₁.

Доказательство

1) Рассмотрим ∆ABC₂, в котором ∠BAC₂=∠A₁ и ∠ABC₂=∠B₁:

∆ABC₂ $\sim$ ∆A₁B₁C₁ (первый признак) => $\frac{AB}{A_1B_1}$ = $\frac{AC_2}{A_1C_1}$ .

2) По условию:

$\frac{AB}{A_1B_1}$ = $\frac{AC}{A_1C_1}$ => AC=AC₂ => ∆ABC = ∆ABC₂ (первый признак) =>
∠B=∠ABC₂=∠B₁ => ∆ABC $\sim$ ∆A₁B₁C₁ (первый признак).

Третий признак

Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого, то треугольники подобны.

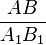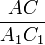Дано: ∆ABC и ∆A₁B₁C₁, $\frac{AB}{A_1B_1}$ = $\frac{AC}{A_1C_1}$ = $\frac{BC}{B_1C_1}$ .

Доказать: ∆ABC 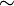$\sim$ ∆A₁B₁C₁.

Доказательство

1) Рассмотрим ∆ABC₂, в котором ∠BAC₂=∠A₁ и ∠ABC₂=∠B₁:

∆ABC₂ $\sim$ ∆A₁B₁C₁ (первый признак) => $\frac{AB}{A_1B_1}$ = $\frac{BC_2}{B_1C_1}$ = $\frac{AC_2}{A_1C_1}$ .

2) По условию:

$\frac{AB}{A_1B_1}$ = $\frac{AC}{A_1C_1}$ = $\frac{BC}{B_1C_1}$ => AC=AC₂, BC=BC₂ => ∆ABC = ∆ABC₂ (третий признак);
∆ABC₂ $\sim$ ∆A₁B₁C₁ => ∆ABC $\sim$ ∆A₁B₁C₁.

Обратная связь

Бесплатный хостинг uCoz