Два выражения (числовые или буквенные), соединённые одним из знаков: «больше» (>), «меньше» (<), «больше или равно» (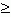
), «меньше или равно» (
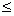) образуют неравенство (числовое или буквенное). Любое справедливое неравенство называется тождественным. Например, тождественны следующие неравенства: 3 · 7 – 20 > 2 · 4 -10, | - 5 | > 3. В зависимости от знака неравенства мы имеем либо строгие неравенства ( > , < ) , либо нестрогие ( 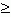, 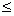). Запись 5a 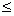4b означает, что 5a либо меньше 4b, либо равно ему. Буквенные величины, входящие в неравенство, могут быть как известными, так и неизвестными. Решить неравенство – значит найти границы, внутри которых должны находиться неизвестные, так чтобы неравенство было справедливым. Решить систему неравенств – значит найти границы, внутри которых должны находиться неизвестные, так чтобы все неравенства, входящие в систему, были справедливы одновременно.
Основные свойства неравенств.
1. Если а > b, то b < а, и, наоборот, если а < b, то b > а.
Доказательство. Пусть а > b. По определению это означает, что число (а — b) положительно. Если мы перед ним поставим знак минус, то полученное число — (а — b) будет, очевидно, отрицательным. Поэтому — (а — b) < 0, или b — а < 0. А это (опять же по определению) и означает, что b < a.
Обратное утверждение предлагаем учащимся доказать самостоятельно.
Доказанное свойство неравенств допускает простую геометрическую интерпретацию: если точка А лежит на числовой прямой правее точки В, то точка В лежит левее точки А, и наоборот (см. рис. 20).
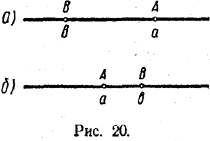
2. Если a > b, a b > c, то а > с.
Геометрически это свойство состоит в следующем. Пусть точка А (соответствующая числу а) лежит правее точки В (соответствующей числу b), а точка В, в свою очередь, лежит правее точки С (соответствующей числу с). Тогда точка А и подавно будет лежать правее точки С (рис. 21).
Приведем алгебраическое доказательство этого свойства неравенств.
Пусть а > b, a b > с. Это означает, что числа (а — b) и (b— с) положительны. Сумма двух положительных чисел, очевидно, положительна. Поэтому (а — b) + (b— с) > 0, или а — с > 0. Но это и означает, что а > с.
3. Если а > b, то для любого числа с а + с > b + с, а — c > b — с.
Иными словами, если к обеим частям числового неравенства прибавить или от обеих частей отнять одно и то же число, то неравенство не нарушится.
Доказательство. Пусть а > b. Это означает, что а — b > 0. Но а — b = (а + с) — (b + с). Поэтому (а + с) — (b + с) > 0. А по определению это и означает, что а + с > b + с. Аналогично показывается, что а — c > b — с.
Например, если к обеим частям неравенства 5 > 4 прибавить 11/2, то получим
61/2 > 51/2. Отнимая от обеих частей данного неравенства число 5, получим 0 > — 1.
Следствие. Любое слагаемое одной части числового неравенства можно перенести в другую часть неравенства, поменяв знак этого слагаемого на противоположный.
Пусть, например, а + b > с. Требуется доказать, что а > с — b. Для доказательства от обеих частей данного неравенства достаточно отнять число b.
4. Пусть а > b. Если с > 0, то аc > bc. Если же с < 0, то ас < bс.
Иными словами, если обе части числового неравенства умножить на положительное число, то неравенство не нарушится;
если обе части неравенства умножить на отрицательное число, то знак неравенства изменится на противоположный.
Короче это свойство формулируется таким образом:
Неравенство сохраняется при почленном умножении на положительное число и изменяет знак на противоположный при почленном умножении на отрицательное число.
Например, умножив неравенство 5 > 1 почленно на 7, получим 35 > 7. Почленное умножение того же неравенства на — 7 дает — 35 < — 7.
Доказательство 4-го свойства.
Пусть а > b. Это означает, что число а — b положительно. Произведение двух положительных чисел а — b и с, очевидно, также положительно, т. е. (а — b) с > 0, или
ас — bс > 0. Поэтому ас > bс.
Аналогично рассматривается случай, когда число с отрицательно. Произведение положительного числа а — b на отрицательное число с, очевидно, отрицательно, т. е.
(а — b) с < 0; поэтому ас — bс < 0, откуда ас < bс.
Следствие. Знак неравенства сохраняется при почленном делении на положительное число и изменяется на противоположный при почленном делении на отрицательное число.
Это вытекает из того, что деление на число с =/= 0 равносильно умножению на число 1/c.
