Показательная функция

Показательная функция — математическая функция 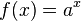, где a называется «основанием», а x — «показателем» степени.
В вещественном случае основание степени — некоторое неотрицательное вещественное (действительное) число, а аргументом функции является вещественный показатель степени.

Пусть  a > 0, {r_n} – последовательность рациональных чисел, сходящихся к x. Определим число a^x как предел

Данный предел не зависит от выбора последовательности r_n, приводящей к числу x. Областью определения показательной функции является вся числовая ось. Эта функция непрерывна, монотонно возрастает при a > 1  и монотонно убывает при 0 < a < 1  Функция никогда не обращается в нуль, но имеет горизонтальную асимптоту  y = 0.

(график 1, график 2)

Основные свойства показательной функции y = a ^x при a > 1:

• Область определения функции - вся числовая прямая.
• Область значений функции - промежуток (0;+).
• Функция строго монотонно возрастает на всей числовой прямой, то есть, если x₁< x_{2 ,} то a^x₁ < a^x₂ .
• При x = 0 значение функции равно 1.
• Если x > 0 , то a ^x > 1 и если x < 0, то 0 < a < 1.