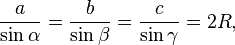Теоре́ма си́нусов — теорема, устанавливающая зависимость между сторонами треугольника и противолежащими им углами. Теорема утверждает, что стороны треугольника пропорциональны синусам противолежащих углов, или, в расширенной формулировке:

Для произвольного треугольника

где a, b, c — стороны треугольника, α,β,γ — соответственно противолежащие им углы, а R — радиус окружности, описанной вокруг треугольника.

Доказательство

Достаточно доказать, что

Проведем диаметр | BG | для описанной окружности. По свойству углов, вписанных в окружность, угол GCB прямой, а угол CGB равен либо α (угол CAB), если точки A и G лежат по одну сторону от прямой BC, либо π − α в противном случае. Поскольку sin(π − α) = sinα, в обоих случаях a = 2Rsinα. Повторив то же рассуждение для двух других сторон треугольника, получаем: